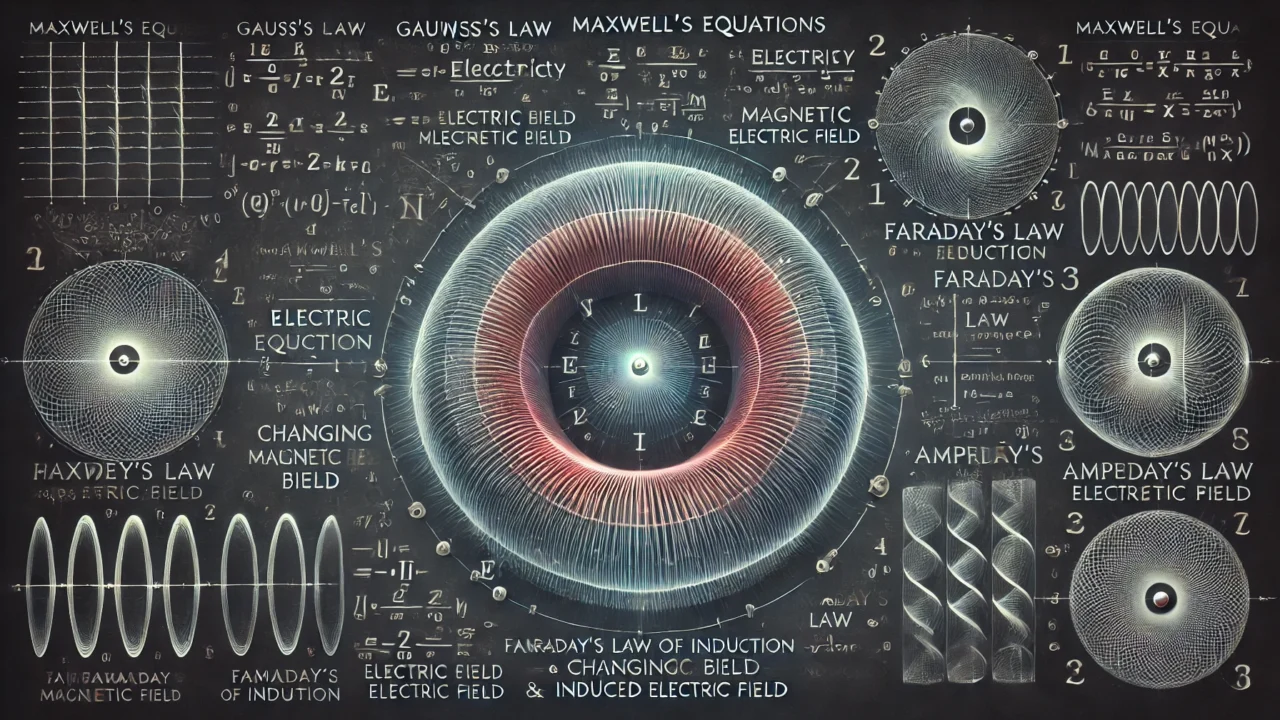
Maxwell’s equations are a set of four fundamental equations in electromagnetism that describe how electric and magnetic fields interact and propagate. These equations are named after James Clerk Maxwell, who first formulated them.
Gauss’s Law for Electricity
Gauss’s law for electricity states that the electric flux through any closed surface is proportional to the total electric charge enclosed within that surface. Mathematically, it is expressed as:
$$ \nabla \cdot \mathbf{{E}} = \frac{{\rho}}{{\epsilon_0}} $$
where \( \nabla \cdot \mathbf{{E}} \) is the divergence of the electric field \( \mathbf{{E}} \), \( \rho \) is the charge density, and \( \epsilon_0 \) is the permittivity of free space.
Gauss’s Law for Magnetism
Gauss’s law for magnetism states that the magnetic flux through any closed surface is zero, implying that there are no magnetic monopoles. This is mathematically written as:
$$ \nabla \cdot \mathbf{{B}} = 0 $$
where \( \nabla \cdot \mathbf{{B}} \) is the divergence of the magnetic field \( \mathbf{{B}} \).
Faraday’s Law of Induction
Faraday’s law of induction states that the induced electromotive force (EMF) around a closed loop is equal to the negative rate of change of the magnetic flux through the loop. In differential form, it is expressed as:
$$ \nabla \times \mathbf{{E}} = -\frac{{\partial \mathbf{{B}}}}{{\partial t}} $$
where \( \nabla \times \mathbf{{E}} \) is the curl of the electric field and \( \frac{{\partial \mathbf{{B}}}}{{\partial t}} \) is the time rate of change of the magnetic field.
Ampère’s Law with Maxwell’s Addition
Ampère’s law with Maxwell’s addition states that the magnetic field around a closed loop is proportional to the electric current passing through the loop and the rate of change of the electric field. This is given by:
$$ \nabla \times \mathbf{{B}} = \mu_0 \mathbf{{J}} + \mu_0 \epsilon_0 \frac{{\partial \mathbf{{E}}}}{{\partial t}} $$
where \( \nabla \times \mathbf{{B}} \) is the curl of the magnetic field, \( \mu_0 \) is the permeability of free space, \( \mathbf{{J}} \) is the current density, and \( \frac{{\partial \mathbf{{E}}}}{{\partial t}} \) is the time rate of change of the electric field.
Derivations and Proofs
Maxwell’s equations can be derived from basic principles of electromagnetism, including Coulomb’s law, the absence of magnetic monopoles, Faraday’s law of induction, and the continuity equation. Here, we outline the derivations briefly.
Derivation of Gauss’s Law for Electricity
Starting from Coulomb’s law, the electric field due to a point charge \( q \) at a distance \( r \) is:
$$ \mathbf{{E}} = \frac{{q}}{{4 \pi \epsilon_0 r^2}} \hat{\mathbf{{r}}} $$
The total electric flux through a spherical surface of radius \( r \) is:
$$ \Phi_E = \oint_{{\text{{surface}}}} \mathbf{{E}} \cdot d\mathbf{{A}} = \frac{{q}}{{\epsilon_0}} $$
Applying the divergence theorem, we get:
$$ \oint_{{\text{{surface}}}} \mathbf{{E}} \cdot d\mathbf{{A}} = \int_{{\text{{volume}}}} (\nabla \cdot \mathbf{{E}}) dV = \frac{{q}}{{\epsilon_0}} $$
Since this holds for any volume, we have:
$$ \nabla \cdot \mathbf{{E}} = \frac{{\rho}}{{\epsilon_0}} $$
Derivation of Faraday’s Law
Faraday’s law can be derived from the experimental observation of electromagnetic induction. If we consider a loop of wire with a changing magnetic flux, the induced EMF is:
$$ \mathcal{E} = – \frac{{d\Phi_B}}{{dt}} $$
Using Stokes’ theorem, the EMF can be related to the electric field:
$$ \oint_{{\text{{loop}}}} \mathbf{{E}} \cdot d\mathbf{{l}} = – \frac{{d}}{{dt}} \int_{{\text{{surface}}}} \mathbf{{B}} \cdot d\mathbf{{A}} $$
Thus, we get the differential form of Faraday’s law:
$$ \nabla \times \mathbf{{E}} = – \frac{{\partial \mathbf{{B}}}}{{\partial t}} $$